Building a key-value store part 1
Designing and building a Redis-like in-memory key-value tree store
Introduction
Have you ever wondered how Redis is so fast? How does it actually persist data to disk? How does it store your keys in memory?
As always, at the end of the post, you can find the link to the repository.
If you follow this publication you probably already guessed that Redis is one of my favorite toys. It can do so many things. But it lacks one thing: storing tree-like data structures such as a binary tree. Technically it can be done but it’s complicated and inefficient.
What’s the logical thing to do? Building our own in-memory key-value tree store that works similarly to Redis. Let’s call it Tedis.
Disclaimer: this is only a toy project to demonstrate some interesting concepts. I haven’t actually browsed Redis’ source code. I just did some research and used common knowledge. In this series, we won’t focus on the distributed nature of Redis so we don’t talk about topics such as consistent hashing. Maybe in a future post.
If you want to try out the end product you can download the binaries here. Check out the project’s README. If there’s a problem you can build your own binaries with make build
The most important features
Redis is incredibly complex, so we pick only a few key features to replicate.
Data structures
For this initial version, I’ll only implement binary search trees. They are one of the most simple trees (except standard binary trees). The following commands will be implemented:
BSTADD key valueadds a new value to the keyBSTMADD key value1 value2 …adds multiple values to the keyBSTREM key valueremoves the specified value from the keyBSTEXISTS key valuereturns true if the value exists, false otherwiseBSTGETALL keyreturns all the nodes as a list
Here are some examples:
BSTADD categories 10
"OK"
BSTADD categories 12
"OK
BSTADD categories 15
"OK"Later, I’m going to explain the basics of binary trees but this one should look like this:
12
/ \
10 15If we now run commands they should act like these examples:
BSTEXISTS categories 12
true
BSTEXISTS categories 19
false
BSTGETALL categories
[12 10 15]Of course, some more tree-specific features can be added later such as calculating the height, returning leaf nodes, returning subtrees, etc. But for now, we’re focusing on the basics.
Append-only log (AOL)
There’s a myth that Redis only stores your data in memory and it can disappear if the server goes bye-bye.
Redis persists your data in two different ways: AOL and RDB. AOL means an append-only log. Whenever you run a CUD (create, update, delete) command a new entry is created in a log file.
You can imagine it like this:
SET foo foo
SET bar bar
DEL fooWhen you start a Redis server this log file is processed and every instruction is executed. Redis basically replays your logs to reconstruct the whole database. The three commands above result in a database with only one key (bar) and one value (bar).
Of course, the exact format is different, but the point is that it contains every command. AOL is the default persistence mechanism of Redis. We’re going to replicate it.
The exact file is called appendonly.aol by default.
RBD (snapshots)
RDB stands for Redis Database. It’s a snapshot of your current dataset. Anything in the memory will eventually persist on the disk after a certain amount of time or number of operations.
It’s a file that contains the values of your keys in a specific format. We can imagine it like this:
key:foo type:string value:foo
key:john type:hash value:firstname:john,lastname:doe,age:23Of course, this format is made up. It’s just an illustration.
There are lots of advantages and disadvantages to both of these solutions. You can read them here. Probably the most important is:
AOL contains everything. It’s the most stable persistent model where data loss is almost impossible. Whenever you execute a command it is appended to the log. With Redis, it can be configured, and the default behavior is that it writes to the log file once a second. But it can changed to “write after every command.”
With RDB you can have data losses since it only persists to the file after X seconds (such as 60). However, the RDB file is usually smaller, and restoring the database from it is usually faster compared to AOL.
Eviction policy
There’s a myth that Redis is quite limited since it stores everything in memory. A typical server has 4-32 GB of RAM. You obviously cannot fit a 100GB MySQL DB into a server that has only 8GB of RAM.
Whenever Redis uses too much memory it will evict (remove) keys that haven’t been used in a while so your server won’t run out of memory. The evicted keys, however, are lost until the next restart. To avoid these situations you can spin up multiple nodes. It’s very easy with managed instances such as Redis Cloud.
The default eviction policy is LRU which stands for Least Recently Used. Let’s say the server has three keys: a,b,c
get a
get b
get c
set d d -> Redis runs out of memory hereSince a is the least recently used key it gets removed and d is set. We will implement this eviction policy.
Go
In this example, I’m going to use Go. If you knew me before Substack you probably knew me as a PHP developer so why am I using Go? Here are two lessons I learned through my career:
Good engineers generally don’t care that much about languages. A language is just a tool. The underlying principle is the same. Memory works the same. CPU works the same. The file system works the same.
In my opinion, you should be able to comfortable read at least the following languages (given that you are a PHP dev): PHP, JavaScript, Java, go, python. They are incredibly popular and easy languages.
On top of that, Go is a pretty good language.
I understand you might not be familiar with it, so here are some of its important features.
No exceptions
When I first started learning Go and I found out they don’t have exceptions I was like: “Well. I’m out of here, thanks.“
I was wrong.
Go is an “errors as values” language. Whenever something goes wrong you get the error as a return value:
result, err := doWork()
if err != nil {
// something went wrong
}This is the same as:
try {
doWork()
} catch (Exception e) {
// something went wrong
}Honestly, it’s not a big deal. I only listed this as the first point because you’re going to see lots of if err != nil in the code examples.
One advantage of this approach is that you have to think about the unhappy case in every case. In lots of languages (such as PHP), you can just ignore catching exceptions. Well, in Go, if a function can go wrong and it returns a tuple (two values, such as in the example above. It’s like a two-element array) you have to accept and handle the error.
Pointers
Go has pointers. Which is a good thing. If you can’t remember, a pointer is just a variable that stores a memory address. The memory address lives in the heap memory and stores the actual value. The pointer can be used to manipulate the value.
It looks like this:
func NewLRU(capacity int) *LRU {
return &LRU{
Capacity: capacity,
Map: make(map[string]string, capacity),
Items: make([]string, capacity),
}
}This function returns a pointer of type LRU. It is expressed in the return value: *LRU. The * can be read as “points to”.
In the body, we return the address of a newly created LRU instance. The address of a variable can be retrieved by &LRU{…} The & can be read as “address of”.
It’s actually not that hard. And don’t worry Go doesn’t have advanced things such as pointer arithmetics, etc. And the language is garbage collected so you don’t have to manually allocate and free up memory.
No classes
Go doesn’t have classes. Don’t worry. They have structs:
type BST struct {
Key string
Root *BinaryTreeNode
}It’s pretty much like a class in other languages. You can also add “methods” to it:
func (tree *BST) Insert(
value int64,
node *BSTNode
) *BinaryTreeNode {
// instead of this.Key tree.Key can be used:
tree.Key
}Normally, a function looks like this:
func Insert()But if you want to associate the function with a struct you need to add the struct as well:
func (tree *BST) Insert()By the way, as far as I know, it’s just syntactic sugar. The Go compiler will inject the BinaryTree instance (or pointer in this case) as an argument to the Insert function.
So the real function looks like this:
func Insert(tree *BST, ...)It’s kind of funny. There are so many OOP concepts such as encapsulation, inheritance, polymorphism, design patterns, solid, etc etc, and Go is like: “let’s just inject it as the first argument.“ Well, it worked.
There’s no inheritance. You can (have to) favor composition over inheritance. There are interfaces and generics.
The last feature is the awesome concurrency model. However, it is very Go-specific so I won’t use it in this post. Maybe in a later article, we’ll talk about it, but for now, let’s focus on the basics.
Probably these are the most important points that can be a little bit weird compared to Java, JavaScript, or PHP.
Binary search trees (BST)
Before we dive deeper, let’s quickly recap what a BST is, and implement some of its important methods.
A binary search tree is a tree that satisfies the following conditions:
Each node in a BST has at most two children, referred to as the left child and the right child
All keys in the left subtree are less than the parent’s value
All keys in the right subtree are greater than the parent’s value
A BST looks like this:
10 is the root element
Each node in the left subtree is smaller than 10
Each node in the right subtree is greater than 10
This rule applies to any node in the entire tree.
Just like any other tree, it’s a node-based data structure:
package trees
type BST struct {
Key string
Root *BSTNode
}
type BSTNode struct {
Value int64
Left *BSTNode
Right *BSTNode
}In Go, nodes are expressed with structs instead of classes.
The BST is a “container” that holds a tree with the root node and a key. Users can access this particular tree via this key.
We’re going to interact with BSTs such as this:
tree := trees.BST{
Key: "my-tree",
}
tree.Add(12)
tree.Add(15)
tree.Add(10)Adding nodes
Inserting a new node is quite simple but it requires recursion (just as everything with trees). Whenever I need to fight with recursion I usually use two methods:
func (tree *BST) Add(value int64) {
tree.Root = tree.add(value, tree.Root)
}
func (tree *BST) add(value int64, node *BSTNode) *BSTNode {
if node == nil {
newNode := BSTNode{Value: value}
return &newNode
}
if value < node.Value {
node.Left = tree.add(value, node.Left)
} else {
node.Right = tree.add(value, node.Right)
}
return node
}The first one is the “entry point” that is exposed to the outside world, and the second one is the one that does the recursion. This way, everything is easier.
In Go, if you start a function with an uppercase letter it is exported. If you start it with a lowercase letter it is not exported to the outside world. So Add() can be called from anywhere, but add() can only be called from the current package.
This shows you why people say Go is a simple language. Uppercase → exported, lowercase → not exported.
<javascript-rant>
Compare this with Javascript:
// #1
const myFunction = () => {
console.log("Hello from myFunction!");
};
const myVariable = 42;
module.exports = {
myFunction,
myVariable,
};
// #2
const myFunction = () => {
console.log("Hello from myFunction!");
};
module.exports = myFunction;
// #3
export const myVariable = 42;
export const myFunction = () => {
console.log("Hello from myFunction!");
};
// #4
const myFunction = () => {
console.log("Hello from myFunction!");
};
export default myFunction;
// #5
const myVariable = 42;
const myFunction = () => {
console.log("Hello from myFunction!");
};
export { myVariable, myFunction };
// #6
(async () => {
const myModule = await import('./myModule.mjs');
myModule.myFunction();
})();I guess there are lots of other ways to do it. I don’t even understand anymore what’s happening in #6.
Go’s decision:
func Exported() {}
func notExported() {}</javascript-rant>
Now let’s talk about the algorithm:
func (tree *BST) add(value int64, node *BSTNode) *BSTNode {
if node == nil {
newNode := BSTNode{Value: value}
return &newNode
}
if value < node.Value {
node.Left = tree.add(value, node.Left)
} else {
node.Right = tree.add(value, node.Right)
}
return node
}When you do recursion, the most important thing is the base case. There’s a point, a condition when you want to stop recursing.
When working with trees, the base case is often:
if node == nilThe function starts with the root node because this is how it’s called:
func (tree *BST) Add(value int64) {
tree.Root = tree.add(value, tree.Root)
}What happens when a tree is empty? The root node will be nil. So the base case immediately applies. What do we want to do when the root is nil? Creating a new node with the value and returning it. So it becomes the root node.
Here’s a simplified version of the code:
func (tree *BST) Add(value int64) {
tree.Root = tree.add(value, nil) // it's an empty tree
}
func (tree *BST) add(value int64, node *BSTNode) *BSTNode {
// let's create a new node and return it
if node == nil {
newNode := BSTNode{Value: value}
return &newNode
}
}And the tree.Root becomes the newly created node’s address.
Now let’s take a look at the if else statement:
if value < node.Value {
node.Left = tree.add(value, node.Left)
} else {
node.Right = tree.add(value, node.Right)
}This is the BST rule:
If the new value is less than the node’s value we need to add it to the left subtree
Otherwise, to the right subtree
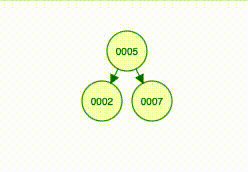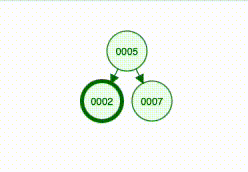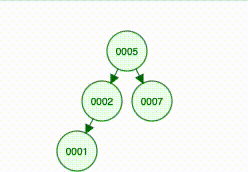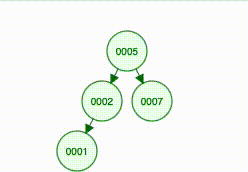
Now think about what happens when we want to add 1 to this tree:
1 is less than 5 so we recurse left
1 is less than 2 so we recurse left
There’s no left child of 2
There comes a point where node.Left (or node.Right) is nil and the function call looks like this:
if value < node.Value {
node.Left = tree.add(value, nil) // no left child
} else {
node.Right = tree.add(value, nil) // no right child
}If that happens the base will apply:
func (tree *BST) add(value int64, node *BSTNode) *BSTNode {
if node == nil {
newNode := BSTNode{Value: value}
return &newNode
}
}So the function creates a new node and returns it. Which will become the last node’s left value because of this line:
if value < node.Value {
node.Left = tree.add(value, nil) // no left child
}So the new node becomes 2’s left child:
And here comes the hardest part:
func (tree *BST) add(value int64, node *BSTNode) *BSTNode {
// ...
return node // <- this line here
}When the function encounters a node that is null, the base case applies. It creates a new node and returns it. But on every other level of recursion, it will reach the last return statement and return the current node.
I always had a hard time understanding recursion when the author showed me a call stack so I’ll try another approach.
This is what happens when the function processes 5 (the root node):
#1
func (tree *BST) add(1, node *BSTNode) *BSTNode {
if 1 < 5 {
{5}.Left = tree.add(1, 2) // 2 is node.Left
}
}It calls itself again:
#2
func (tree *BST) add(1, node *BSTNode) *BSTNode {
if 1 < 2 {
{2}.Left = tree.add(1, nil) // nil is node.Left
}
}Now Left is nil so it hits the base case:
#3
func (tree *BST) add(1, node *BSTNode) *BSTNode {
if node == nil {
newNode := BSTNode{Value: 1}
return &newNode
}
}And now #3 returns to #2 after the if statement:
func (tree *BST) add(1, node *BSTNode) *BSTNode {
if 1 < 2 {
{2}.Left = tree.add(1, nil) // nil is node.Left
}
// it continues here
return {2}
}The return statements return the node with the value of 2.
And now #2 returns to #1 after the if statement:
func (tree *BST) add(1, node *BSTNode) *BSTNode {
if 1 < 5 {
{5}.Left = tree.add(1, 2) // 2 is node.Left
}
// it continues here
return {5}
}And now there is no more add() in the call stack so the program returns to Add():
func (tree *BST) Add(value int64) {
tree.Root = {5}
}So thanks to the last return statement it all pops back to the root node.
Retrieving all elements
When it comes to trees we can traverse them in two ways:
Depth-first search (DFS)
Breadth-first search (BFS)
DFS traverses each subtree until its leaf node. In other words, it goes down.
BFS traverses each level. In other words, it goes from left to right.
Given this tree:
DFS will output: [5 2 1 7 6 8]. It always processes the left subtrees first. This is why the output is [5 2 1] which is the most-left subtree and then [7 6] and finally [8]. DFS comes in 3 different variations: pre-order, in-order, and post-order. We’re not going into details, but the one I showed you is pre-order. In-order produces [1 2 5 6 7 8], while post-order outputs [1 2 7 6 8 5]
BFS will output: [5 2 7 1 6 8]. [5] is the first level. [2 7] is the second. And finally [1 6 8] are the leaf nodes.
DFS is implemented with recursion, so it uses the call stack. BFS on the other hand uses a FIFO queue. Since recursion is not involved, let’s do BFS.
BFS works like this:
It starts at the root element
We push it onto a queue
There’s a loop that runs until the queue is empty
In each iteration, the first element is popped out of the queue
In each iteration, we push the left and the right child onto the queue
Given the same tree:
The queue looks like this in every iteration:
#1
We push the root: [5]
loop starts
#2
The first element is popped: []
current = 5
Children of 5 are pushed: [2 7]
Output: 5
#3
The first element is popped: [7]
current = 2
Children of 2 are pushed: [7 1]
Output: 2
#4
The first element is popped: [1]
current = 7
Children of 7 are pushed: [1 6 8]
Output: 7
#5
The first element is popped: [6 8]
current = 1
Children of 1 are pushed: [6 8]
Output: 1
#6
The first element is popped: [8]
current = 6
Children of 6 are pushed: [8]
Output: 6
#7
The first element is popped: []
current = 8
Children of 8 are pushed: []
Output: 8The final output (or return value) will be [5 2 7 1 6 8]. In this algorithm, the current level’s nodes are always the first items in the queue.
The implementation is quite simple:
func (tree *BST) GetAll() []int64 {
queue := make([]*BSTNode, 0)
if tree.Root != nil {
queue = append(queue, tree.Root)
}
values := make([]int64, 0)
for len(queue) > 0 {
current := queue[0]
queue = queue[1:]
values = append(values, current.Value)
if current.Left != nil {
queue = append(queue, current.Left)
}
if current.Right != nil {
queue = append(queue, current.Right)
}
}
return values
}In Go, an array (slice) or hashmap can be created with the make() function:
queue := make([]*BSTNode, 0)This line creates a *BSTNode array (slice). 0 is the initial size. Since we don’t know how many elements will be stored in the queue 0 is fine. It will grow as necessary.
After that, it pushes the root node to the queue and creates a new array (slice) called values. This is going to be the return value.
Then the loop starts. First, it gets and removes the first item. Go doesn’t offer array functions such as array_shift which does these two things in one go. Instead, we need to do this:
current := queue[0]
queue = queue[1:]The first line returns the first element. The second one removes it. queue[1:] means “return every element from index 1.”
After that, the code is pretty self-explanatory:
values = append(values, current.Value)
if current.Left != nil {
queue = append(queue, current.Left)
}
if current.Right != nil {
queue = append(queue, current.Right)
}if there’s a left child push it onto the queue. Do the same with the right child. It basically pushes the next level onto the queue.
That’s it! We can add and get items to and from a binary search tree.
Check out the repository here.
To be continued
We haven’t even started talking about “Redis-specific” features but this post is already getting too long.
I soon publish the next parts. Don’t worry, we won’t do tree-specific stuff anymore.
If you have questions, don’t forget to leave a comment: